经验误差与过拟合
概念
错误率:分类错误的样本数占样本总数的比例。
精度:1 - 错误率。
训练误差(经验误差):学习器在训练集上的误差。
泛化误差:学习器在新样本上的误差。
过拟合:把训练样本自身的一些特点当作了所有潜在样本都具有的一般特征。一般无法彻底避免,只能缓解。
欠拟合:与过拟合相反,即对训练样本的一般性质未学习好。
评估方法
留出法
留出法(hold-out)直接将数据集D划分为两个互斥的集合,其中一个集合用作训练集S,另一个作为测试集T。即D=S∪T,S∩T=Ø。
其缺点在于少了一部分数据,所以训练出来的模型必然会有一定的偏差。
交叉验证法
交叉验证法(cross validation)先将数据集D划分为k个大小相似的互斥子集,即D=D1∪D2∪…∪Dk,Di∩Dj=Ø(i ≠ j)。每个子集都尽可能保持数据分布的一致性,即从D通过分层采样获得。然后每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;这样可获得k组训练/测试集,从而可进行k次训练和测试,最终返回的是这k个测试结果的均值。通常将其称为“k折交叉验证”。k的最常用取值为10,此时称为10折交叉验证。
其缺点在于时间复杂度会提升,k折即需要训练k次,在高复杂度的算法中,就会有较大影响。
自助法
自助法是基于自助采样法(bootstrap sampling)。其过程为:每次随机从D中挑选出一个样本,将其“拷贝”到D1(注意是拷贝,即D1中的数据仍然可以在下一次采样中采集到),这个过程重复执行m次后,我们就得到了包含m个样本的数据集D1。
显然,D中的一部分样本会在D1中出现多次,也可能一次都不出现。
做一个简单的估计,某一样本x在m次采样中都不出现的概率为:(1 - 1//m)m,取极限可得其大概为 1/e = 0.368。即,初始样本集D中约有36.8%的样本未出现在采样集D中D1中,所以我们将D1作为训练集,D/D1作为测试集。这样,实际的评估模型与期望评估的模型都使用了m个训练样本。而仍然有1/3的数据样本没出现在训练集中,可以用于测试。
该方法一般用于样本数量较小,难以有效划分训练集/测试集时。
缺点:改变了初始数据集的分布,这会引入估计偏差。
性能度量
性能度量是指衡量模型泛化能力的评价标准。
错误率与精度
见上文
查准率、查全率与F1
| 真实情况 | 预测情况 | |
| 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
则查准率 P与查全率R分别为:
P = TP / (TP + FP)
R = TP / (TP + FN)
即查准率为预测正例中真实也正例的比例。
查全率为真实情况为正例中预测也为正例的比例。
查准率和查全率是一对矛盾的度量。
P-R图中面积越小则性能越好。
平衡点(BEP)为 查准率 = 查全率时的取值。
F1 = (2 * P * R)/ (P + R) = (2 * TP) / (样本总数 + TP - TN)
更一般的形式Fβ:
Fβ = [(1 + β2) * P * R] / [(β2 * P) + P]
实际上F1是基于查准率与查全率的调和平均(harmonic mean):
1 / F1 = (1 / 2) * (1 / P + 1 / R)
同样,Fβ则是加权调和平均:
1 / Fβ = 1 / (1 + β2) * (1 / P + β2 / R)
ROC与AUC
ROC全称为“受试者工作特征”(Receiver Operating Characteristic)曲线。
其纵轴为“真正例率”(True Positive Rate,简称TPR)
横轴为“假正例率”(False Positive Rate,简称FPR)
即:
TPR = TP / (TP + FN)
FPR = FP / (TN + FP)
AUC(Area Under ROC Curve)即ROC曲线下的面积。
代价敏感错误率与代价曲线
一般对于不同的类别,我们错误的预测会造成不同的后果。例如把患者诊断为健康人和把健康人预测为病人,显然前者的后果更加严重。基于此,我们给出以下表格来定义不同的样本之间错误预测的代价:
| 真实情况 | 预测情况 | |
| 第0类 | 第1类 | |
| 第0类 | 0 | cost01 |
| 第1类 | cost10 | 0 |
所谓代价敏感错误率即要最小化所有样本预测的cost均值最小化。即:
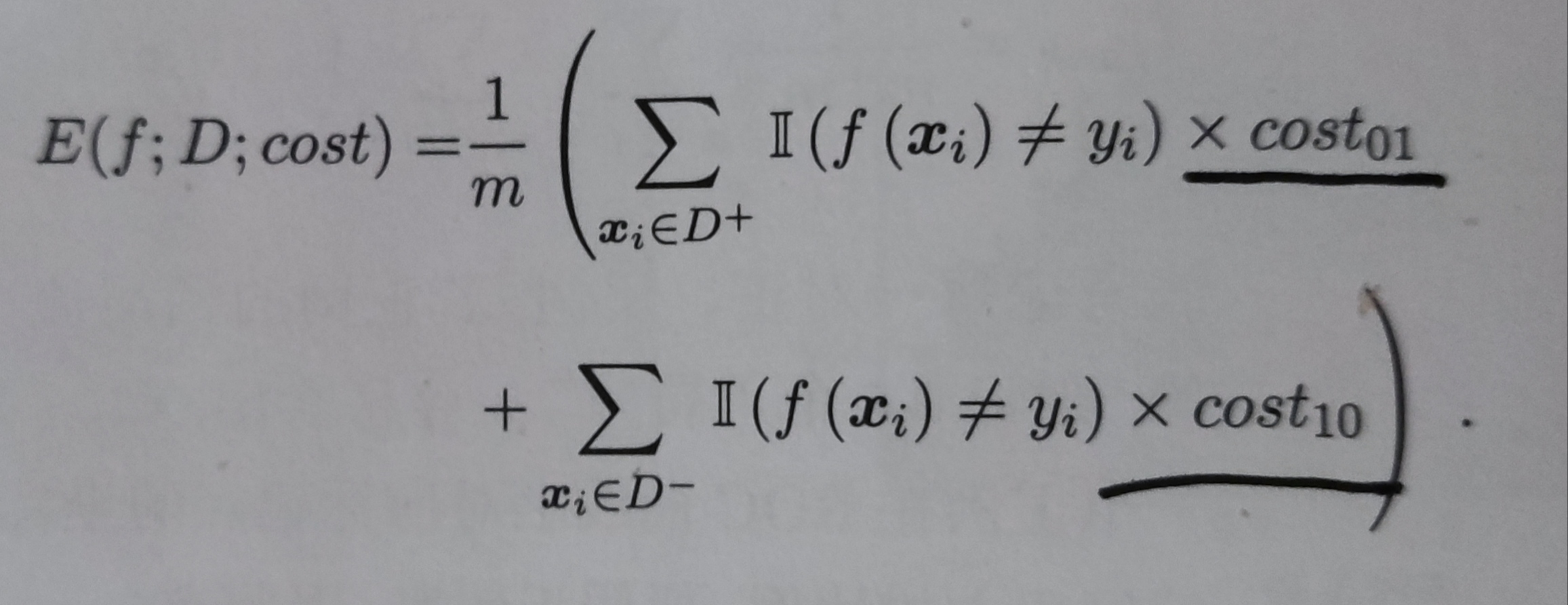
注:假定上表中的第0类为正例,第1类为反例,令D+与D-分别代表样例集D的正例子集和反例子集
在非均等代价下,ROC曲线不能直接反映出学习器的期望总和代价,而代价曲线(cost curve)可以达到该目的。
其横轴为正概率代价:
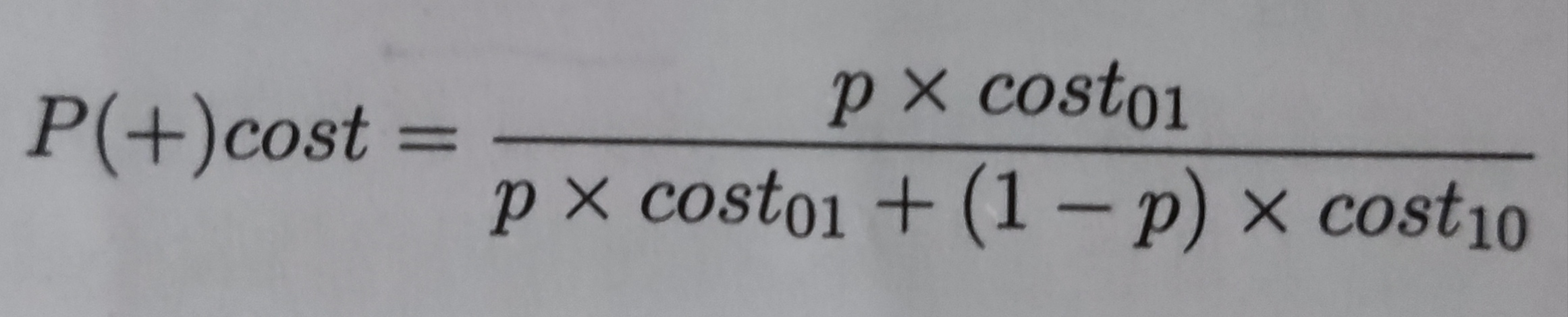
其中p是样例为正例的概率。
纵轴是取值为[0, 1]的归一化代价。
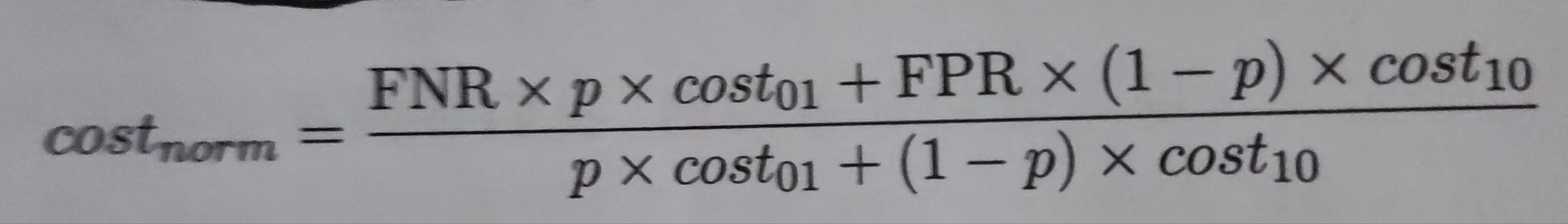
其中FPR为上面提到的假正例率,
FNR = 1 - TPR是假反例率
